Question
Implement a binary tree with a method getRandomNode() that returns a random node.
eg.
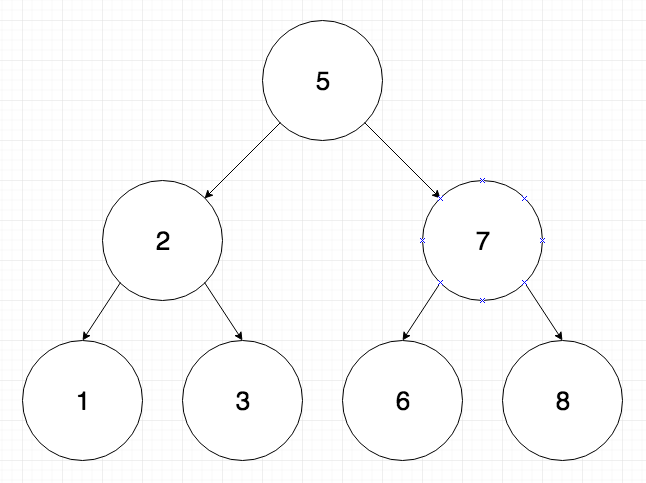
|
1 2 3 |
getRandomNode() = 5 getRandomNode() = 8 getRandomNode() = 1 |
Once you think that you’ve solved the problem, click below to see the solution.
As always, remember that practicing coding interview questions is as much about how you practice as the question itself. Make sure that you give the question a solid go before skipping to the solution. Ideally if you have time, write out the solution first by hand and then only type it into your computer to verify your work once you've verified it manually. To learn more about how to practice, check out this blog post.
Solution
How was that problem? You can check out the solution in the video below.
Here is the source code for the solution shown in the video (Github):
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 |
// Individual node of the tree private class Node { Node left; Node right; int val; int children; } // The root of the tree private Node root; private Random rand; // Return each node with probability 1/N public int getRandomNode() { if (root == null) throw new NullPointerException(); // This is an index of a node in the tree. Indices go in sorted order. int count = rand.nextInt(root.children + 1); return getRandomNode(root, count); } // Recursive method. Binary search through tree to find the index. We use // the number of children to determine which direction to go private int getRandomNode(Node curr, int count) { if (count == children(curr.left)) return curr.val; if (count < children(curr.left)) return getRandomNode(curr.left, count); // The new index becomes the index of the same node but now within the // subtree rather than the whole tree return getRandomNode(curr.right, count - children(curr.left) - 1); } // Return the number of nodes in a given subtree private int children(Node n) { if (n == null) return 0; return n.children + 1; } |
Did you get the right answer to this coding interview question? Please share your thoughts in the comments below.