There are lots of hard coding interview questions, but recursion is by far one of the most feared topics. And not without good reason…
After all, recursion is really kind of a double whammy. First of all, it’s counterintuitive. We don’t tend to think about things in a recursive way. And then on top of that, unless you’re one of the few people out there who uses Haskell or another functional language, you simply never actually use recursion in the real world.
That means that in your coding interviews, you need to be able to apply a confusing skill that you never use. No wonder recursion is a challenge.
In this post, I want to change that.
The fact of the matter is that recursion doesn’t have to be difficult. In this post, I’m going to show you some real-world examples of recursion.
Why? Because understanding these real-world examples will help you to see how recursion really works and help you understand why you should care. Rather than being this abstract thing you need to learn just for your interviews, you can understand how it actually applies in all these different instances.
And if you’re bored, did I hear someone say “side project ideas”?…
File Trees and Parsing
Imagine that you want to find a file on your machine. You don’t want to look for it manually, and you figure this is a good exercise anyway, so you’re going to write a function to find it for you. How do you approach this?
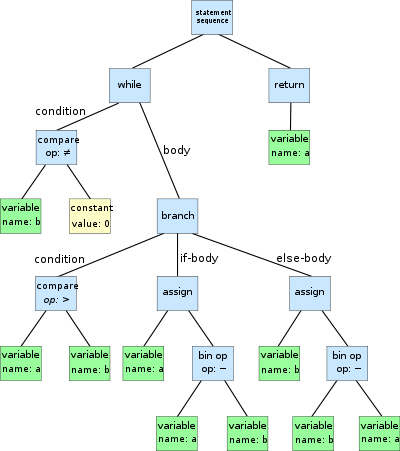
We’ll start with the root directory. Then we need to pick one of the children and look inside. That child might have its own children, so we have to go deeper and deeper until there are no more children. Then we go back and try one of the other children.
What did we just do?
Our code might look something like the following:
|
1 2 3 4 5 6 7 8 |
func search(currentDir): if targetFile in currentDir: return currentDir for childDir in currentDir: result = search(childDir) if result != null: return result return null |
Does this look familiar at all?
We started in our current directory and then made a recursive call for each child directory. We called our function within itself to search through the child directory.
Basically, we’re doing depth-first search.
This is a very simplified example, but it illustrates something very important: Recursive structures are all around us.
Any time we have any sort of hierarchical structure, the easiest approach for us to parse through that structure will be to use recursion.
Simply put, recursion allows us to easily keep track of what we’ve already traversed and saves us the effort of having to track, for example, which directories we’ve visited before. Recursion allows us to follow a well-defined progression through our directories.
Another common example of where we might want to use recursion to parse a hierarchy is when working with syntax trees or HTML.
Imagine that we want to update all of the divs in our HTML document to have a specific class. Maybe that class is dependent on where the div is in the document. By far the easiest approach is to recursively traverse the tree.
You might immediately say, “Why don’t we just do a string search on our HTML document?” Valid question.
The great benefit of going through the actual syntax tree and parsing recursively is that we always have context of where we are. Say we want to set the class based on the class of the wrapping div. When we do it recursively, it becomes easy.
Game Solvers
If you’ve ever taken a machine learning class, game solving algorithms are likely familiar to you. There are tons of games out there that can be approached with some form of depth-first search.
Although the problem space can get pretty huge pretty fast, we could play chess, checkers, Sudoku, and so many more games just by considering all possible moves and searching for those that will allow us to win.
Even when we start to get fancier by using a algorithm like A* search, the fundamentals are the same. All we’re doing with A* is using a heuristic to prune our set of possible moves so that it doesn’t expand so dramatically.
Let’s consider an example of a simple game such as Sudoku.

At its core, Sudoku is a very simple game. All we have to do is find the appropriate combination of numbers so that each square contains the digits 1-9 exactly once and each line meets the same criteria.
If we want to solve the game, the simplest approach would be to just find all possible combinations of numbers and then try to validate which combination is the correct one. The validation part is easy; we just check the preconditions described above.
Finding all the combinations is relatively trivial as well if we have a good understanding of recursion. I’ll cover this briefly here, but you can find a lot more information under the “Selection” section of my article “Recursion for Coding Interviews: The Ultimate Guide.”
Essentially, the approach that we are going to take is to go through each cell one at a time and assign it a possible value. Then we recursively assign all possible values to all remaining cells.
Our code might look something like this (Note: I’ve numbered the cells 0-81 so that I can convert the 2D matrix into a 1D array):
|
1 2 3 4 5 6 7 8 |
func sudoku(currentCell): if (currentCell == 81) return [[]] remainingCombinations = sudoku(currentCell+1) results = [] for (combination in remainingCombinations): for i = 1 to 9: results.add(combination.prepend(i)) return results |
Protip: If you’re confused about how this works, I encourage you to walk step-by-step through the code as shown in this video.
With this simple code, we are able to generate every possible combination of values on the sudoku board.
Of course, we can continue to make optimizations here. We don’t have to look at every combination because we could preemptively identify which combinations can’t possibly be valid. This is where we would use backtracking to improve our approach.
While this is a simplistic example, recursion is clearly integral to solving many types of games. If you’re looking for a small side project to practice recursion, this is a good way to go.
Fractal Designs

Not only can recursion be used for internal computations, but we can also visualize recursion by generating fractal patterns.
Fractal patterns are patterns that are defined recursively. Simply put, the pattern is made up of smaller and smaller versions of the same pattern.
One of the hard things about recursion is that it tends to be a very opaque topic. Not only is it hard to understand what the code itself is doing, but it’s hard to even understand how the code executes.
There are so many layers of complexity that following along becomes very difficult. Therefore, if you are struggling with recursive problems, experimenting with fractal designs is a great introduction that allows you to see the fruits of your labor.
Rather than going in-depth here, I will refer you to one of the assignments from Princeton University’s Intro to Computer Science class. The exercises here are well thought out and a great place to practice drawing with recursion.
Inductive Proofs

If you’ve never studied computer science theory, you may not be super familiar with inductive proofs. However, they are a fascinating tool, particularly for proving that recursive solutions to problems are actually correct. It can also be helpful for understanding how recursion might apply in the real world.
So for starters, what is an inductive proof?
Basically, an inductive proof is composed of two basic parts (these might seem familiar if you compare it to recursion):
- The base case
- The inductive step
The base case is simply something that we can demonstrate to be true for a particular value (P(0)). We only have to prove the single case, so we can just show validity for that one example.
The inductive step shows that we can get from P(n) to P(n+1). Rather than spend lots of time talking about the math, let’s look at a few examples.
Climbing a Ladder:
What is the base case? Simply, can we climb onto the first rung of the ladder? This is easy to prove by demonstration.
What is the inductive step? Can we get from one rung of the ladder to the next with a goal of some arbitrary rung on the ladder? Obviously, there are real world limitations in this example, since the ladder can’t be infinitely tall and rungs could be missing or unevenly spaced, but assuming some perfect, infinitely long ladder, then the answer is yes.
With these two components, we have proven that we can climb from the ground to any rung on the ladder.
1+2+…+(n-1)+n == n(n+1)/2
Now, let’s look at a more classic mathematical example. This is a common formula that we learn in math class, so let’s prove that it is actually true for all values of n.
First off, what is our base case?
If we’re trying to prove that this holds true for all natural numbers, then our base case should be P(1), since it will be the smallest natural number.
So does 1 = 1(1+1)/2? Yes it does.
And what about our inductive step?
Well, we want to say that P(n+1) = P(n) + (n+1), right? We know that if n increases by 1, then our function result should also increase by n+1.
In this example, we can just expand everything and do a bit of algebra:
(n+1)(n+1+1)/2 ?= n(n+1)/2 + (n+1)
(n+1)(n+2) ?= n(n+1)+2(n+1)
n2+3n+2 ?= n2+n+2n+2
n2+3n+2 == n2+3n+2
Now we can see that our inductive step holds true regardless of what the value of n is. Since that is true and our base case is true, we know that our formula is true for any natural number.
Unlock Recursion With Real-World Applications
Recursion is hard. There are no two ways about it. But that doesn’t mean it has to be completely opaque and incomprehensible.
With the examples we discussed here, you now have many applications that you can use to experiment with recursion and try it for yourself.
If you’re struggling with recursion, I’d highly encourage you to experiment. See what works and what doesn’t. Implement one of these real-world applications. Remember that practice makes perfect.